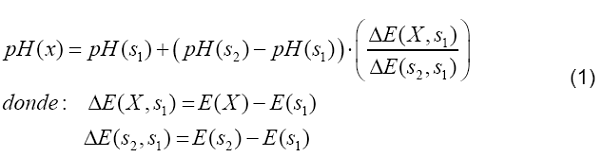
10. ANEXOS: EJEMPLOS DE ESTIMACIÓN DE INCERTIDUMBRE:

Se les recuerda que las estimaciones de incertidumbre deben realizarse conforme a la Guía GUM, se adjuntan ejemplos de estimación de incertidumbre.

Ejemplo 1: Determinación del valor de la actividad del ión hidronio en una muestra incógnita:

Se desea determinar el valor de la actividad del ion hidronio, en una muestra incógnita, realizando la curva de pH con dos disoluciones amortiguadoras de 4,00 ± 0,02 y 7,00 ± 0,02, a 25 °C, considerando solamente los aportes a la incertidumbre, producto del modelo matemático.

Modelo matemático

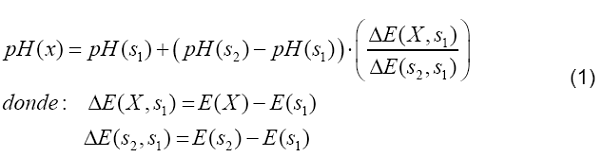
Donde:

pH(s1) = valor de pH de la disolución amortiguadora 1

pH(s2) = valor de pH de la disolución amortiguadora 2

E(X) = potencial en mV, de la muestra

E(s1) = potencial en mV, de la disolución amortiguadora 1

E(s2) = potencial en mV, de la disolución amortiguadora 2

Resultados experimentales

pH(s1)= 4,00                 s1)=167,9 mV

pH(s2)= 7,00                 s2)=- 4,0 mV

E(X)= 158,2 mV

A partir de los datos anteriores determinó que el valor de la actividad de ion hidronio en la muestra es de: pH(X) = 4,169

Las variables de entrada pueden ser observadas en la figura 1

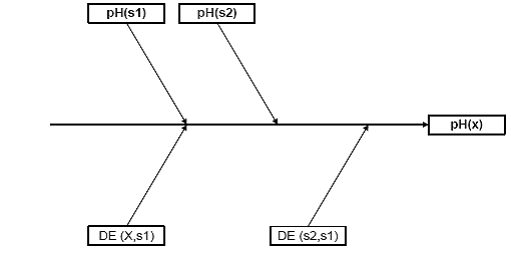
Figura 1. Gráfico de causa- efecto, para el modelo matemático (1)

Para determinar la incertidumbre estándar de la determinación, utilizamos la siguiente fórmula:

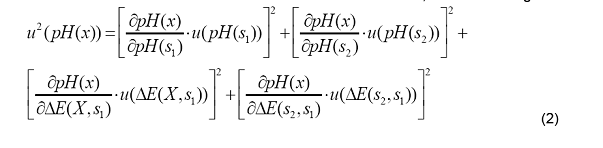
Donde son los coeficientes de sensibilidad

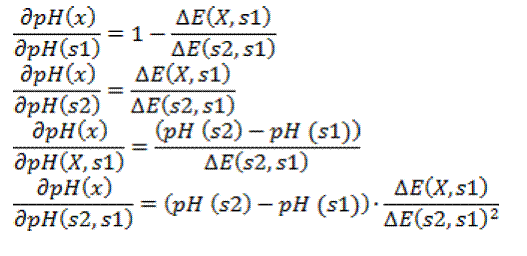
Por lo tanto, al sustituir los resultados experimentales en las ecuaciones de coeficientes de sensibilidad, tenemos:

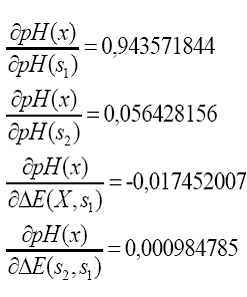12121()

Para determinar la incertidumbre estándar de cada variable, debo considerar la información suministrada por el fabricante o determinada experimentalmente, en nuestro caso específico solamente consideramos al fabricante. No existe información suficiente, que me indique que la tolerancia indicada por el fabricante de las soluciones amortiguadoras y la tolerancia del potenciómetro, tienen alguna distribución específica, por lo tanto considero que las mismas tienen distribución rectangular.

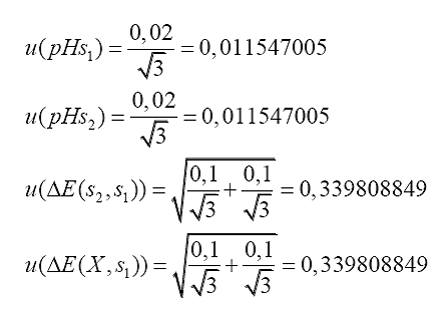
Finalmente, sustituyo y obtengo la incertidumbre estándar

Ejemplo 2. Cálculo de incertidumbre asociado a las contribuciones sobre una magnitud obtenida por medición directa.

Determinación de la incertidumbre combinada asociada a una determinación de masa en una balanza analítica digital con resolución de 0,5 mg.

Indicación del instrumento

m = 2,3050 g

Contribuciones a la incertidumbre:

a. incertidumbre estándar por calibración:

Tolerancia por calibración (linealidad) = 0,00015 g

Distribución = rectangular

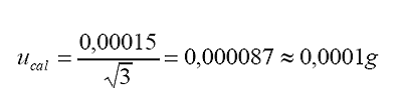
b. incertidumbre estándar por lectura en escala digital:

Tolerancia por lectura (resolución digital) =0,0005 g

Distribución = rectangular

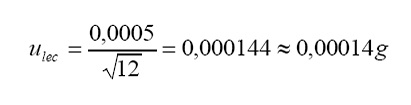
Cálculo de incertidumbre:

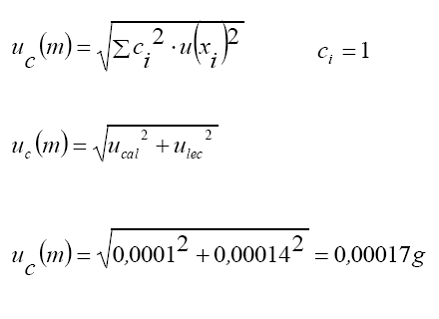
Reporte de resultado:

m = 2,3050 g,               uc = 0,00017 g

Ejemplo 3: Cálculo de incertidumbre asociado a las contribuciones sobre una magnitud

obtenida por medición directa.

Ejemplo:

Determinación de la incertidumbre combinada asociada a la operación de medición y vertido de un volumen de 10,0 mL utilizando una pipeta graduada con capacidad máxima de 20,0 mL.

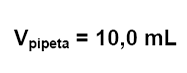
Contribuciones a la incertidumbre:

a. Incertidumbre estándar por tolerancia del fabricante a 20 °C:

Tolerancia por calibración = . 0,03 mL

Distribución = triangular

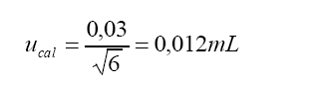
b. incertidumbre estándar por lectura de la escala graduada:

La incertidumbre asociada al proceso de lectura de la escala de una pipeta graduada se determina a partir de la resolución de la escala graduada.

Resolución de la escala:

Mínima división de escala = 0,02 mL

Factor de ojo = 2

Distribución = rectangular

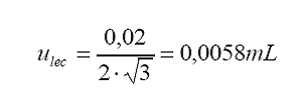
c. Incertidumbre estándar por diferencia entre la temperatura de calibración (20 °C) y la temperatura de trabajo:

Variación máxima de temperatura alrededor de 20 °C = .3 °C

Coeficiente de expansión térmica del agua = 2,1.10-4 °C-1

Distribución = rectangular

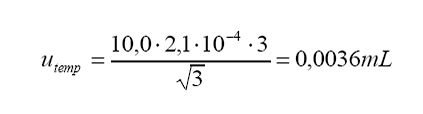
d. Repetibilidad:

s=0,025 (desviación estándar a partir de 7 réplicas)

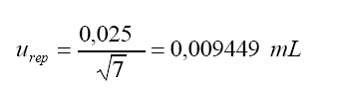
Cálculo de incertidumbre combinada:

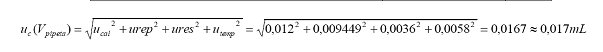
Reporte de resultado:

Vpipeta = 10,00 mL, uc = 0,017 mL

Ejemplo 4: Cálculo de la incertidumbre asociada a una cantidad obtenida mediante una

operación fundamental tipo multiplicación y/o división.

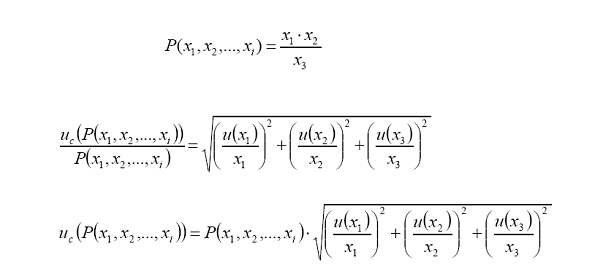
Ejemplo:

Determinación de la incertidumbre asociada a la concentración de una disolución de KCl obtenida al disolver 0,2350 g de KCl en balón aforado de 100,0 mL.

Contribuciones a la incertidumbre:

a. Incertidumbre estándar asociada a la balanza analítica.

incertidumbre estándar por calibración:

Tolerancia por calibración (linealidad) = 0,00015 g

Distribución = rectangular

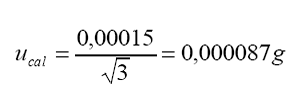
Incertidumbre estándar por lectura en escala digital:

Incertidumbre por lectura (resolución digital)

Distribución = rectangular

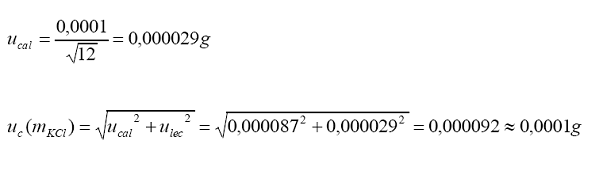
b. Incertidumbre estándar asociada al peso molecular.

c. Incertidumbre estándar asociada a la pureza.

Tolerancia del fabricante = 0,005 (98,0 . 0,5 %)

Distribución = rectangular

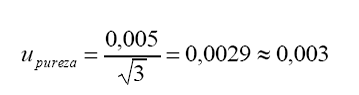
d. Incertidumbre estándar asociada al balón aforado.

Incertidumbre estándar por calibración del fabricante a 20 °C:

Tolerancia por calibración = .0,1 mL

Distribución = triangular

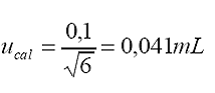
incertidumbre estándar por lectura de la marca de aforo:

Reproducibilidad = 0,035 (desviación estándar a partir de 5 réplicas)

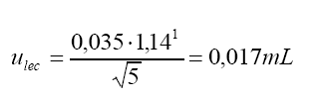
¹ estadístico t para 4 grados de libertad y 68% de confianza.

Incertidumbre estándar por diferencia entre la temperatura de calibración (20 °C) y la

temperatura de trabajo:

Variación máxima de temperatura alrededor de 20 °C = .3 °C

Coeficiente de expansión térmica del agua = 2,1.10-4 °C-1

Distribu ción = rectangular

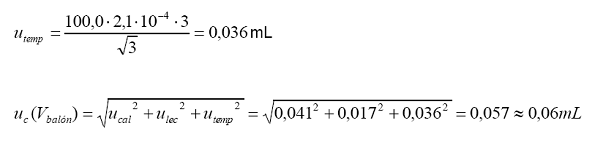
Cálculo de incertidumbre:

Reporte del resultado:

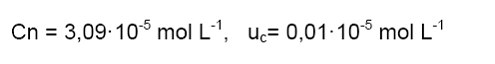
Ejemplo 6: Determinación de la concentración promedio de cierto componente x en un alimento mediante la técnica de espectrofotometría ultravioleta. Luego de seguir el procedimiento indicado, el cálculo de la concentración del componente x se obtiene según la fórmula:

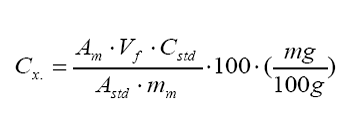
En términos de la absorbancia, masa y volumen final de la muestra.

Los resultados obtenidos para tres muestras del alimento se indican en la siguiente tabla:

1. Cálculo de concentración y análisis de incertidumbre para la muestra #1:

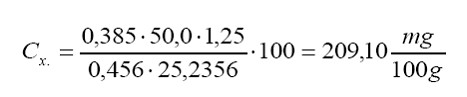
A_m = absorbancia de la muestra.

Am = 0,385.

Contribuciones a la incertidumbre calculadas como de costumbre:

A_std = absorbancia del estándar.

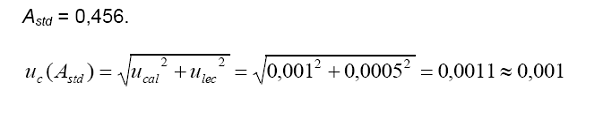
C_std = concentración del estándar del componente x, preparado a partir de un estándar  sólido certificado según se indica:

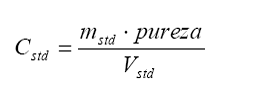
donde m_std es la masa del estándar sólido de cierta pureza reportada, la cual ha sido disuelta hasta un volumen final V_std:

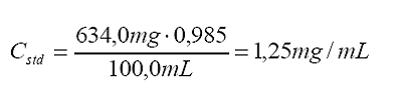
contribuciones de incertidumbre calculadas como de costumbre:

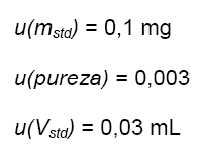
V_f = volumen final de la muestra (balón aforado).

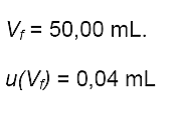
m_m = masa de la muestra.

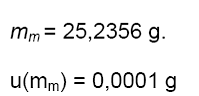
Cálculo de incertidumbre:

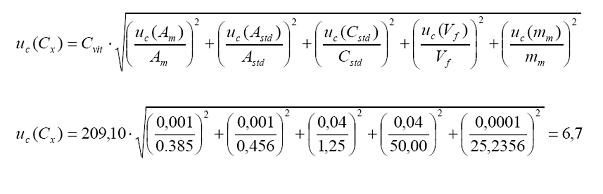
2. Cálculo e incertidumbre de la concentración promedio del componente x:

Un procedimiento de cálculo similar aplicado a las otras dos muestras permite obtener los resultados resumidos en la siguiente tabla:

De donde se obtiene el valor de la concentración promedio con su respectiva incertidumbre estándar:

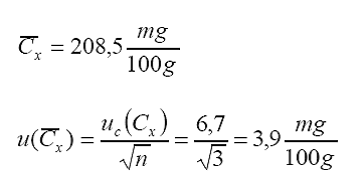
Para completar el cálculo de incertidumbre del valor promedio se debe de tomar en cuenta la contribución por repetibilidad. Esta se calcula en términos del desvío estándar de las réplicas respecto del valor promedio:

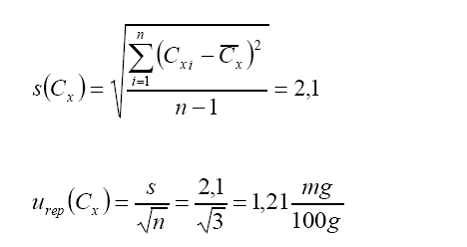
Ahora el cálculo de la incertidumbre estándar combinada total del valor promedio será ahora:

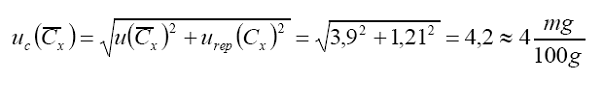
Reporte de resultado:

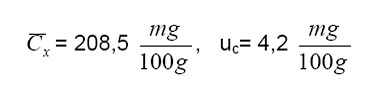
incertidumbre expandida a un 95% de confianza =

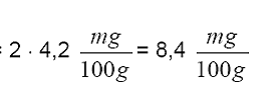
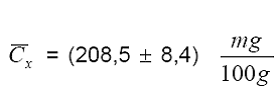 = con un factor de cobertura k=2, que indica un nivel de confianza de aproximadamente el 95 %.